Today, I would like to extend my previous topic on discrete probability distribution with the concept of Binomial Distribution.
A binomial distribution is a specific probability distribution. It is used to model the probability of obtaining one of two outcomes, a certain number of times k out of fixed number of trials N of a discrete random event. A binomial distribution has only two outcomes: the expected outcome is called a success and any other outcome is a failure. The probability of a successful outcome is P and the probability of a failure is 1 – P.
The below rules must be followed:
Rule #1: There are only two mutually exclusive outcomes for a discrete random variable (i.e. success or failure).
Rule #2: There is a fixed number of repeated trials (i.e., successive tests with no outcome excluded).
Rule #3: Each trial is an independent event (meaning the result of one trial doesn’t affect the results of subsequent trials).
Rule #4: The probability of success for each trial is fixed (i.e., the probability of obtaining a successful outcome is the same for all trials).
Real life use of Binomial Distribution:
- Product quality control test.
- Product buy frequency test.
- Employee performance factor analysis.
Formula of Binomial Distribution to calculate mean and standard deviation:
The mean of a binomial distribution with parameters N (the number of trials) and π (the probability of success on each trial) is:
μ = Nπ
where μ is the mean of the binomial distribution. The variance of the binomial distribution is:
σ2 = Nπ(1-π)
where σ2 is the variance of the binomial distribution.
Probabilities for a binomial random variable X can be found using the following formula for p(x):
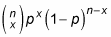
In general, to calculate “n choose x,” one may use the following formula:

Hope you liked my post. Stay tuned for more.